Is Picking Two Marbles Permutation

In our case we get 336 permutations from above and we divide by the 6 redundancies for each permutation and get 336 6 56.

Is picking two marbles permutation.

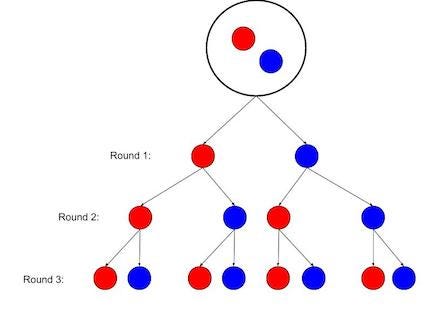
Two marbles are drawn without replacement. You remove them from the bag one of the time without replacement. A draw the tree diagram for the experiment. There are 4 red marbles 3 yellow 2 green and 1 blue marble.

If we want to figure out how many combinations we have we just create all the permutations and divide by all the redundancies. B find probabilities for p bb p br p rb p ww p at least one red p exactly one red 3. A jar contains 4 black marbles and 3 red marbles. In this case you know whether both are red after the first step so the second step is not necessary and you can work with combinations.

Two marbles are drawn without replacement from a jar containing 4 black and 6 white marbles. For permutations without repetition we need to reduce the number of objects that we can choose from the set each time. There s two green marbles in the bag. Algebra permutations solution.

Fancy word for just a simple idea that the sample. For example given that we have 5 different colored marbles blue green red yellow and purple if we choose 2 marbles at a time once we pick the blue marble the next marble cannot be blue. There s one blue marble. Suppose an opaque jar contains 4 red marbles and 10 green marbles the following exercise refers to the experiment of picking two marbles from the jar without replacing the first o log on.

If we randomly select two marbles from the bag what is the probability that the selected marbles are of different colors in other words one white and one red. Assuming each color of marble is identical and it doesn t matter which specific marble of each color is chosen calculate the number of possible permutations in which you can remove the 10 marbles. Endgroup jessica oct 6 13 at 3 36. And then there s one blue marble in the bag.

So this is all the possible outcomes. So i could pick that green marble or that green marble. 1 after marble no 2 is different from vice versa. Selecting k objects from n objects is given by.

It is crucial that you are choosing items without replacement for the two methods to be equivalent. Why do the two solutions differ. So if we have 3 tin cans to give away there are 3. Or 6 variations for every choice we pick.

Choosing a first marble then a second is the same as first choosing two marbles then picking which goes first.